Parallax Mapping
CS 381 Lecture, Dr. Lawlor
So far, we've been drawing everything with simple polygons. But
polygons are flat; and often we want to simulate curved or bumpy
surfaces. A common approach is to use a fragment shader to
make a polygon not look like a polygon--to make it look like a chunk of bark, or a piece of a curved sphere.
Bump Mapping
A really common trick is to use a texture map to store a shift
in the polygon's normal vectors. This "bump mapping" makes a
smooth polygon look rough, and works great under various lighting
conditions. Because a bump map only stores deviations in
the normal, a single bump map texture can be applied to several
different objects. Because you want to be able to increase or
decrease a normal's components, but texture colors are always positive,
it's common to store bump map deviations with 0.5 added to them.
Then in the fragment shader, you compute the normal like this:
vec3 N = normalize(
polygonNormal +
(texture2D(bumpTex,texCoords)-vec4(0.5))
);
There's one annoying problem with bump mapping, which is that the
deviations to a normal are really best expressed in a surface-local
coordinate system (a "tangent space" coordinate system). We'll
talk more about tangent space when we talk about models.
Normal Mapping
If the surface gets bumpy enough, or if we'd like to use several
different polygon models of the same object ("level of detail" models,
for example), it's common to store the whole normal in a texture,
called a "normal map". This is actually simpler than bump
mapping, and it means the polygon's normal isn't even needed.
vec3 N = normalize(
(texture2D(bumpTex,texCoords)-vec4(0.5))
);
You were actually doing normal mapping in HW5.
Parallax Mapping
But bump mapping or normal mapping only affect lighting--the surface
still "moves" like it's totally flat. One solution is to
subdivide each polygon into lots of smaller polygons (often called
"displacement mapping"), but polygons are expensive. Lately,
computer graphics researchers have been playing with techniques to make
polygon surfaces appear to have actual height variations, and move
appropriately.
The simplest of these approaches is called "Parallax Mapping". This is a quite recent technique, proposed by Taichi et al in a short 2001 paper. My favorite way to do parallax mapping is a bit different from Taichi's.
We start at the polygon's surface. We'd like to shift the texture
coordinates so it looks from the camera like we're rendering a
"virtual" surface at a height h from the original polygon.
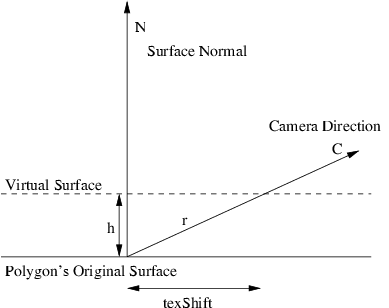
The surface normal is N, the camera direction is C, and the surface
height is the scalar h. Our problem is to compute the shift in
texture coordinates, texShift.
The first thing to notice is that if the angle between N and C is t
radians, then assuming the virtual surface makes a right angle to the
(original) surface normal,
cos(t) = h / r
If N and C are unit vectors, this means
dot(N,C) = h/r
And so rearranging,
r = h / dot(N,C)
Now, r gives the distance we need to move along the camera direction. What we need is the distance to move in texture coordinates.
We can always convert the scalar r into a 3D shift in world coordinates
by multiplying by the camera direction C. But then we need to
convert a shift in 3D world coordinates into a shift in 2D texture
coordinates.
It's simplest to do this if texture coordinates are some simple
function of world coordinates. Then a variation in world
coordinates corresponds to some simple variation in texture
coordinates.
For example, if
texCoords = 7.0 * worldCoords;
then texture coordinates are just seven times world coordinates, and a
world-coordinates shift of "off" is a texture-coordinates shift of
"7.0*off". In general, if
texCoords = f(worldCoords)
then we just need to compute the derivative of each component of f
along each direction in world coordinates, and multiply the derivative
vector by the world-coordinates shift. It's best to compute these
"texture shift from world shift" vectors wherever you assign texture
coordinates--usually either in your vertex shader or in C++.
So overall, assuming "texX" and "texY" are the derivatives of the X and
Y texture-coordinates-from-worldspace functions, then we can just dot
the world coordinates offset to get a texture coordinates offset:
texShift = vec2(dot(texX,off), dot(texY,off));
And overall our parallax mapping code is just three lines:
float r=h/dot(N,C); /* distance along camera vector to move */
vec3
off=C*r;
/* world-coordinates movement from polygon surface to virtual surface */
vec2 texShift=vec2(dot(off,texX),dot(off,texY));
You can see this in action in my parallax mapping demo code
(Zip, Tar-gzip).
Parallax mapping usually looks best when combined with bump or normal mapping;
this way both lighting and texture correspond to the moved surface.
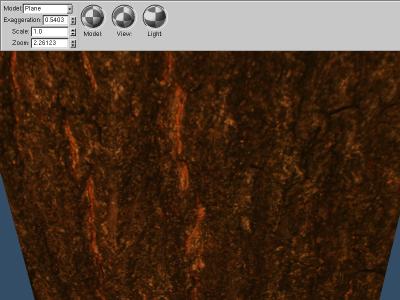
Parallax Mapping Only
|
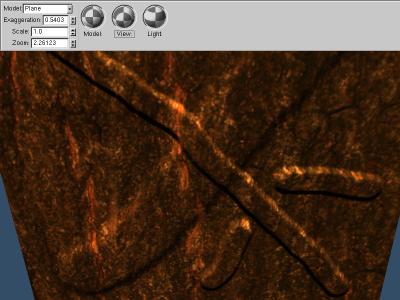
Parallax and Normal Mapping
|

Normal Mapping Only
|
Parallax mapping is tough to see in a static image...






