Iterated Function Systems

CS 481/681 2007 Lecture, Dr. Lawlor

An Iterated Function System (IFS) is a really simple object. It's just a small set of matrices, or other space-to-space functions (hence usually called "maps"). It's really easy to describe lots of interesting fractal shapes using IFSs, where the shape consists of nothing but a set of scaled copies of itself. That is, an IFS is a definition for a sort of "recursive object", where you define the object in terms of smaller copies of itself.

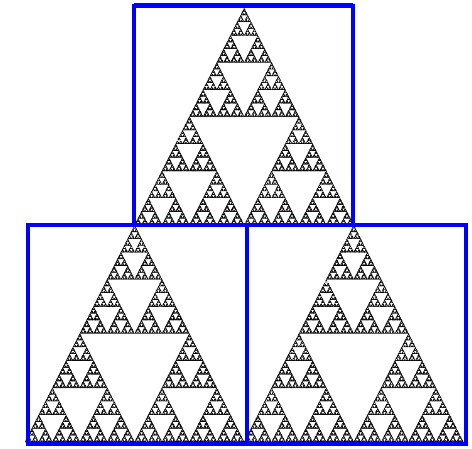
For example, a Sierpinski Triangle consists of three smaller Sierpinski Triangles. Hence you can represent a Sierpinski Triangle using an IFS with 3 matrices that map the unit square down onto the three pieces.

You can draw an IFS by recursively applying the IFS matrices, like this. Eventually you do need a recursive base case, where you draw a point or dot or... anything, really!

void drawSierpinski(Matrix cur) {
	if (coordinates_are_really_small(cur)) 
	{ /* Recursion base case: draw a little dot at this coordinate origin */
		draw_a_point(cur);
	} else { /* Recursion case */
		drawSierpinski(cur*top_and_center);
		drawSierpinski(cur*down_and_left);
		drawSierpinski(cur*down_and_right);
	 }
}

Or if you've got a list of matrices, the same recursion looks like this:

void drawIFS(Matrix cur,int level,const std::vector<Matrix> &matrices) {
	if (level>10) 
	{ /* Recursion base case: draw a little dot at this coordinate origin */
		draw_a_point(cur);
	} else { /* Recursion case */
		for (int m=0;m<matrices.size();m++)
			drawSierpinski(cur*matrices[m], level+1, matrices);
	}
}

What's really weird about IFSs is that *there is no geometry there*. It's all just points, defined by a small set of matrices.

Curiously, you can also draw an IFS without recursion by applying a randomly chosen IFS matrix to a randomly-chosen point:

void diceIFS(const std::vector<Matrix> &matrices) {
	Point p=Point(0,0);
	for (int i=0;i<1000000;i++) {
		p=matrices[rand()%matrices.size()] * p;
		draw_a_point(p);
	}
}

You can define IFSs in any number of dimensions; see some 3D examples in an online Java Applet.

I wrote a paper in late 2002 describing how to find bounding volumes for 2D and 3D IFS. The same page has presentations, a much nicer 2D IFS editor than my 3D version on the course homepage, and a whole set of cool 2D IFSs.