Terrain Simplification

CS 481/681 2007 Lecture, Dr. Lawlor

Terrains are big. That's what you want them for--to make your world keep rolling on and on.

But terrains can be big. That's the problem--they stuff your graphics card with piles of little teeny polygons way off in the distance, even stuff behind you.

For example, say you want 1m terrain resolution. That's actually pretty coarse. Say you want a 2km view distance. That's a grid 4km on a side, centered on the camera. So that's 16 million grid cells, or 32 million triangles. Now at 30fps, you're talking 900 million polygons per second. That's well beyond the capabilities of all existing graphics cards.

But:

Half the geometry is behind your head, and another substantial fraction is off the sides of the window. So we need "view culling".
Most of the polygons are really far away and tiny; only the really nearby ones are actually needed. So we need "level of detail".

Luckily a single technique can provide both view culling and level of detail--recursive bounding.

Recursive Bounding

There's a really simple powerful data structure we'll be using--a spatial subdivision tree. Each node of the tree represents a certain region of space. The child nodes of that tree represent a subset of that region of space. To draw a tree node, you:

First figure out if you can even see the tree node. If you can't, forget it--you don't even have to think about any of the node's children. This automatically gives you view culling.
Next figure out if it's worthwhile to draw the children. If you're far enough from the camera that your whole node is only a few pixels across (for some definition of "few", normally 0.5 to 50 pixels), then just draw some approximation of your terrain and return. This gives you level of detail--big quads far away, and little quads up close.
Otherwise you have to draw your children. Recurse onto each of them. If you just recurse in the right order, you can automatically get back-to-front ordering (for the painter's algorithm) or front-to-back ordering (for early-Z exit).

Spatial trees are everywhere. You don't need very much at each node--a set of pointers to the child nodes, and some sort of bounding volume. I like using bounding spheres.

Geometric Complications

Unfortunately, anywhere the terrain is nonlinear (that is, pretty much everywhere!) your big and little quads aren't going to match up along their boundaries. There are several interesting ways to handle this:

You can generate a gappy mesh, then add a "cleanup" step where you fill in the gaps using little "skirts" of triangles. The trickiest part about this is keeping track of where you need skirts, and where you don't.
Lindstrom's terrain method has a cool way of generating big and little quads using triangles that doesn't require any runtime size tracking--you essentially bake the gap-filling into your error data structure, and at runtime if you follow certain rules to generate triangles, then you'll never end up with gaps.

So once you understand the basics, DO NOT IMPLEMENT YOUR OWN TERRAIN ALGORITHM. Use one of the many existing nice libraries (collection by Stefan Röttger).

Geodetic Complications

Sadly, your average planet is curved. Over a room, that doesn't make much difference, and you can draw the room as if the world is flat. Over just a few dozen kilometers, the curvature of the Earth induces a several-meter height shift--the center of the elevation map is lifted due to the curve of the Earth:

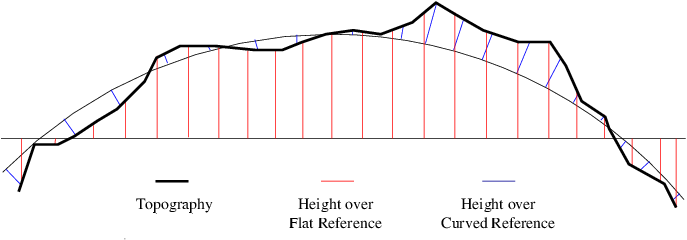
Terrain surface over flat and curved references

Terrain surface over flat and curved references

It is possible to resample a heightfield specified across a map-friendly curved reference to a heightfield specified across a computation-friendly flat reference--this involves both a height change and a location shift. You can also write your heightfield code carefully, and handle curved reference surfaces automatically.

Be aware that the "0.0m above sea level" surface is NOT a sphere, and not even an ellipsoid, it's a "geoid", whose shape depends on annoying nonmathematical entities such as mountain ranges (whose gravitational attraction tilts the sea, as well as all plumb bobs!).

Luckily, for scenes smaller than about four kilometers across, the Earth's curvature amounts to less than 1/3 meter, which can usually be safely ignored.