Pretty Pictures, OpenGL, Taylor Series, and Physics

CS 480 Lecture, Dr. Lawlor

Pretty Pictures of Simulations

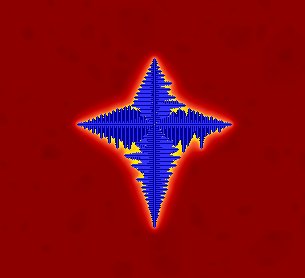
Ice simulation
Ice solidification simulation.  Red is the liquid area, with temperature shown shading to yellow (hottest).  Blue is solidified crystal; I get to choose the crystal planes, in this case just cartesian axes.

Fluid dynamics simulation
A fluid dynamics simulation: white paint sheared between layers of darkness.

Simple beam in bending

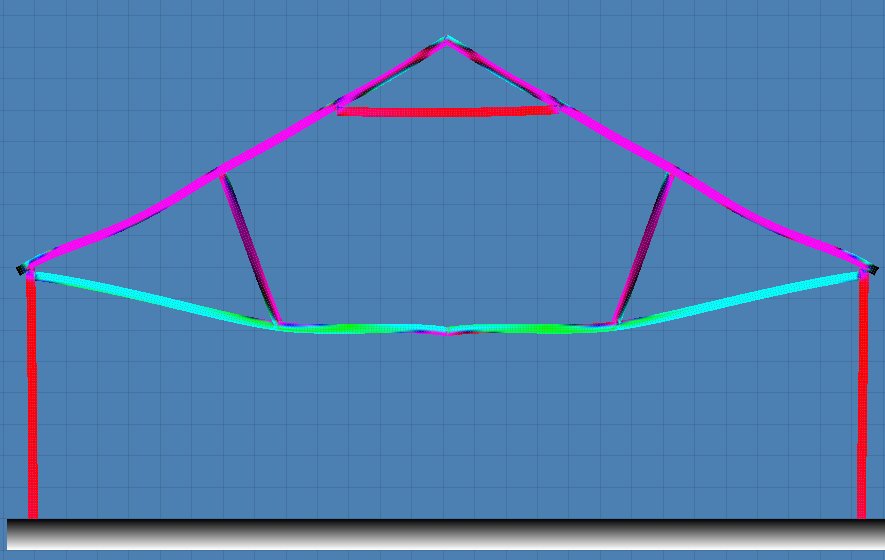
Bending in a wooden structure
A finite element solid mechanics simulation: wood in compression (red), tension (green), and shear (blue).  Gray gradients are fixed.  Unlike most of my simulations, this one is actually dimensioned properly, and verified against the real world!

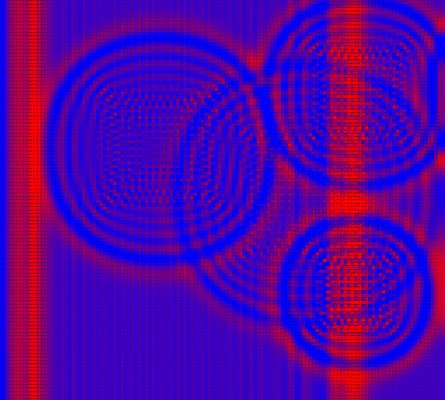
Drops of liquid expanding outward    More drops
A shallow water simulation, like drops on a pond.  The little drops expand outward, pass through one another, and reflect off the walls.

Reaction-diffusion face
A photograph toned using reaction-diffusion equations.

Basic OpenGL Particle Rendering

Here's a tiny OpenGL program to splat some random points onto the screen:
/**
  Tiny OpenGL/GLUT example program
  Dr. Orion Sky Lawlor, olawlor@acm.org, 2009-01-21 (Public Domain)
*/
#include "GL/glut.h" /* windows, mice, etc.  http://freeglut.sourceforge.net */
#include <stdlib.h> /* for "rand" */
#include <stdio.h> /* for printf */

/* Random Float: Return a random number between 0 and 1 */
float rf(void) { return (rand()&0xffff)*(1.0/0xffff); }

void display(void) /* Draw everything in our window */
{
	glClearColor(0.3,0.5,0.7,1.0); /* clear to a nice blue color */
	glClear(GL_COLOR_BUFFER_BIT);
	
	glBegin(GL_POINTS);
	srand(1);
	for (int p=0;p<100000;p++) {
		glColor3f(rf(),rf(),rf());
		glVertex3f(2*rf()-1,2*rf()-1,2*rf()-1);
	}
	glEnd();
	
	glutSwapBuffers(); /* display everything we've rendered so far */
	glutPostRedisplay(); /* continual animation */
}

int main(int argc,char **argv) {
	glutInit(&argc,argv);  /* set up GLUT */
	glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGBA | GLUT_DEPTH);
	glutCreateWindow("TinyDemo"); /* make a window */
	glutDisplayFunc(display); /* here's how to draw the window */
	glutMainLoop(); /* start drawing */
}
If that wasn't crystal clear, work your way through the NeHe tutorials on OpenGL!

Taylor Series

Check out the MathWorld article, or Wikipedia.