Bounding Volume Hierarchies and Iterated Function Systems
2010, Dr. Lawlor, CS
481/681, CS, UAF
Basically, every raytracer looks like this code:
for (each pixel) {
for (each ray bounce) {
for (each chunk of geometry) {
if (ray from pixel hits geometry)
shade pixel with geometry
}
}
}
The performance is clearly going to be
O(pixels*bounces*geometry). The number of pixels is in the
millions, the amount of geometry is in the thousands, although luckily
we can get away with only a few bounces (on average). Searching
thousands of chunks of geometry for each of the millions of pixels per
frame is not going to be efficient.
One simple way to improve performance above is to reduce the number of
pixels--that is, reduce the screen resolution. Another simple
trick is to reduce the geometric complexity of the scene.
But one surprising way to reduce the average geometric complexity per ray without changing the final image is to use a "bounding volume hierarchy".
The basic idea behind bounding volumes is before digging into a
complicated block of geometry, we first intersect our ray with a simple
bounding volume like a sphere. If the ray misses the sphere, then
we can skip the entire block of geometry. Because misses are
common (a ray can only hit one object in the end!), this can be a huge
savings in complex scenes. You can even have a nested tree of
bounding volumes, and raytracing then boils down to something like a
binary search: does the ray hit anything on the left? No, how
about the right? Yes! Then is it the left-right, or the
right-right? And so on.
Common bounding volumes include:
- Planes. Intersecting a ray with a plane only takes one dot
product, but you need to load the plane normal and offset, which is
four floats. Planes aren't closed, so you need several planes to
bound small objects.
- Bounding boxes. Intersecting a ray with an axis-aligned bounding box takes three dot products, and six floats.
- Spheres. Intersecting a ray with a sphere takes three dot products, and four floats.
In pseudocode, you traverse the bounding volume tree to find all the geometry that intersects a ray like this:
ray_intersection intersect(ray r,geometry_tree_node g) {
ray_intersection ret=miss;
for (c in child geometry of g) {
if (r hits c's bounding volume)
add_intersection(ret,intersect(r,c));
}
return ret;
}
Of course, "intersect" is a recursive function, and recursion isn't
supported on the GPU yet (no hardware stack). Instead of
recursing, you can:
- Ignore bounding volumes, and just traverse all the geometry
linearly. The bounding volumes give you a log-factor speedup,
like binary search, so this is quite expensive for scenes with any
complexity.
- Expand the functions out to a fixed recursion depth. The code grows exponentially as you do this, though!
- Convert the recursion to some form of iteration. For example, you can add links to "thread" a binary tree, which allows you to traverse the tree without using any stack space.
Building a bounding volume hierarchy requires the scene geometry to be
pre-processed into a search tree. But we can see much of the same
behavior with "recursive geometry" such as an iterated function system.
Iterated Function Systems: Recursively Defined Geometry
An iterated function system (IFS) is a set of "map" functions that
transform a parent bounding volume into a set of child bounding
volumes. You can draw an IFS by recursively applying the map
functions, which gives smaller and smaller bounding volumes. For
example, here's a Sierpinski Triangle, which is defined as three
smaller Sierpinski triangles:
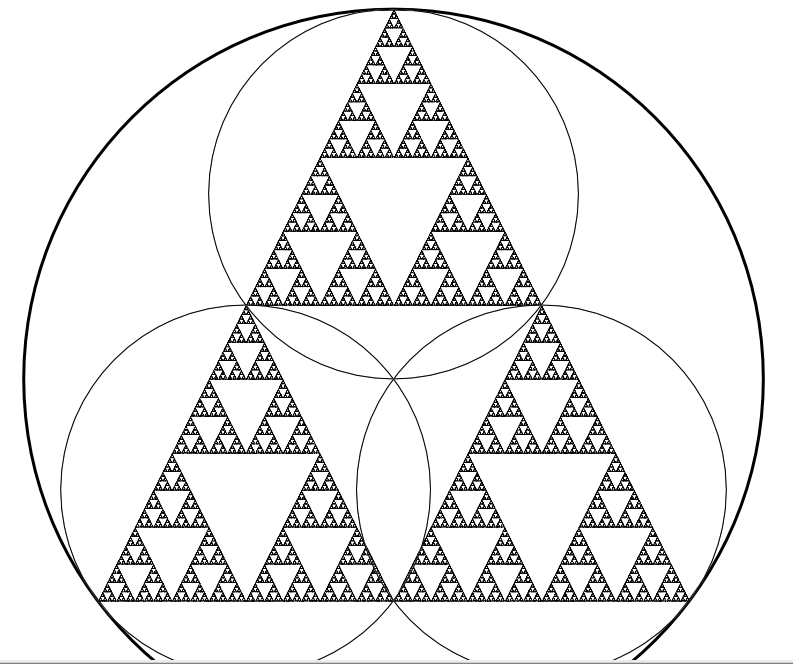
You can read much more about iterated function systems online, for example the Wikipedia Sierpinksi page.
I wrote a little 2D IFS manipulation program back in 2003.
