
vec4 grid(vec2 loc) {
vec2 gridcorner=floor(loc);
vec2 gridfrac=loc-gridcorner;
if (gridfrac.x<0.5 ^ gridfrac.y<0.5)
return vec4(1,0,0,1); // red
else
return vec4(0,0,0,1); // black
}
void main(void) {
gl_FragColor=grid(texcoords*10.0);
}

vec4 grid(vec2 loc) {
vec2 gridcorner=floor(loc);
vec2 gridcenter=gridcorner+vec2(0.5);
float radius=length(loc-gridcenter);
if (radius<0.3)
return vec4(1,0,0,1); // red
else
return vec4(0,0,0,1); // black
}
void main(void) {
gl_FragColor=grid(texcoords*10.0);
}

vec4 grid(vec2 loc) {
vec2 gridcorner=floor(loc);
vec2 gridcenter=gridcorner+vec2(0.5);
float radius=length(loc-gridcenter);
if (radius<0.3)
return texture2D(tex1,texcoords); // read texture 3
else
return vec4(0,0,0,1); // black
}
void main(void) {
gl_FragColor=grid(texcoords*10.0);
}

vec4 grid(vec2 loc) {
vec2 gridcorner=floor(loc);
vec2 gridcenter=gridcorner+vec2(0.5);
float radius=length(loc-gridcenter);
if (radius<0.3)
return texture2D(tex1,gridcenter*0.1); // read texture 3
else
return vec4(0,0,0,1); // black
}
void main(void) {
gl_FragColor=grid(texcoords*10.0);
}
You can even move the dots, again by fetching a dot-center based shift
vector. Note that I can only shift the circle's center so far,
until it begins to hit the boundaries between grid cells. Here,
with a radius=0.3 circle, I can shift the center to lie between between
0.3 and 0.7, and the entire circle stays inside my grid cell.
vec4 grid(vec2 loc) {
vec2 gridcorner=floor(loc);
vec2 gridshift=0.4*texture2D(tex1,gridcorner*0.1234);
vec2 gridcenter=gridcorner+vec2(0.3)+gridshift;
float radius=length(loc-gridcenter);
if (radius<0.3)
return texture2D(tex1,gridcenter*0.1); // read texture 3
else
return vec4(0,0,0,1); // black
}
void main(void) {
gl_FragColor=grid(texcoords*10.0);
}
To move dots farther than one grid cell, I need to search over all the adjacent grid corners: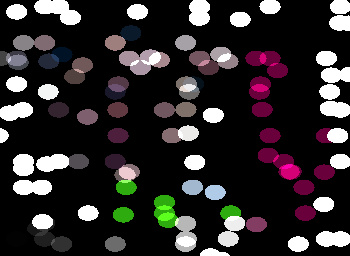
vec4 grid(vec2 loc) {
vec4 ret=vec4(0.0);
vec2 gridcorner=floor(loc);
for (float dy=-1.0;dy<=1.0;dy++)
for (float dx=-1.0;dx<=1.0;dx++)
{
vec2 thiscorner=gridcorner+vec2(dx,dy);
vec2 gridshift=2.4*texture2D(tex4,thiscorner*3.456);
vec2 center=thiscorner+vec2(-0.7)+gridshift;
float radius=length(loc-center);
if (radius<0.3)
ret+=texture2D(tex1,center*0.1);
}
return ret;
}
With this approach, just the distance to the nearest grid cell actually
looks fairly interesting, giving a series of dots reminiscent of a voronoi diagram. This is a "cellular" texture; read more about these at gamedev (for pretty pictures).
vec4 grid(vec2 loc) {
float dist=10.0; // distance to closest grid cell
vec2 gridcorner=floor(loc);
for (float dy=-1.0;dy<=1.0;dy++)
for (float dx=-1.0;dx<=1.0;dx++)
{
vec2 thiscorner=gridcorner+vec2(dx,dy);
vec2 gridshift=texture2D(tex4,thiscorner*3.456);
vec2 center=thiscorner+gridshift;
float radius=length(loc-center);
dist=min(radius,dist);
}
return vec4(dist);
}
Here's the distance to the *second* nearest grid point; I had to expand
my search radius slightly to find points. This effect is
described in Worley's 1996 paper.
vec4 grid(vec2 loc) {
float dist=10.0; // distance to closest grid cell
float second=10.0; // distance to the next-nearest grid cell
vec2 gridcorner=floor(loc);
for (float dy=-2.0;dy<=2.0;dy++)
for (float dx=-2.0;dx<=2.0;dx++)
{
vec2 thiscorner=gridcorner+vec2(dx,dy);
vec2 gridshift=texture2D(tex4,thiscorner*3.456);
vec2 center=thiscorner+gridshift;
float radius=length(loc-center);
if (radius<dist) { // new best
second=dist;
dist=radius;
} else if (radius<second) {
second=radius; // new second-best
}
}
return vec4(second*0.7);
}
Here's the distance to the second-nearest point, minus the distance to
the nearest point, which gives a cool stained-glass effect.
vec4 grid(vec2 loc) {
float dist=10.0; // distance to closest grid cell
float second=10.0; // distance to the next-nearest grid cell
vec2 gridcorner=floor(loc);
for (float dy=-2.0;dy<=2.0;dy++)
for (float dx=-2.0;dx<=2.0;dx++)
{
vec2 thiscorner=gridcorner+vec2(dx,dy);
vec2 gridshift=texture2D(tex4,thiscorner*3.456);
vec2 center=thiscorner+gridshift;
float radius=length(loc-center);
if (radius<dist) { // new best
second=dist;
dist=radius;
} else if (radius<second) {
second=radius; // new second-best
}
}
return 2.0*vec4(second-dist);
}
void main(void) {
gl_FragColor=grid(texcoords*10.0);
}
Another recurring feature is "multi-octave" effects. For example, here's a single repeating texture; a high note:vec4 grid(vec2 loc) {
return texture2D(tex4,loc);
}
void main(void) {
gl_FragColor=grid(texcoords*10.0);
}
Here's the same texture stretched out to a lower frequency:
vec4 grid(vec2 loc) {
return texture2D(tex4,loc*0.5);
}
void main(void) {
gl_FragColor=grid(texcoords*10.0);
}
Here are the two, added together:vec4 grid(vec2 loc) {
vec4 high=texture2D(tex4,loc);
vec4 low=texture2D(tex4,loc*0.5);
return 0.5*(high+low);
}
void main(void) {
gl_FragColor=grid(texcoords*10.0);
}
 Here are many octaves added together (this looks better with a noisy repeating image):
Here are many octaves added together (this looks better with a noisy repeating image):vec4 grid(vec2 loc) {
vec4 ret=vec4(0.0);
for (float freq=8.0;freq>=0.25;freq*=0.5)
ret+=texture2D(tex4,loc*freq);
return (1.0/6.0)*ret;
}
void main(void) {
gl_FragColor=grid(texcoords);
}

void main(void) {
float cx=texcoords.x, cy=texcoords.y; // location onscreen
float x=cx, y=cy; // point to iterate
float r=0.0; // radius of point (squared)
for (int i=0;i<100;i++) //<- repeat!
{
float newx=x*x - y*y;
y=2*x*y; // <- complex multiplication
x=newx+cx; y=y+cy; // bias by onscreen location
r=x*x+y*y; // check radius
if (r>4.0) break;
}
gl_FragColor=vec4(x,r*0.1,y,0);
}