Parallel Reductions
CS 441/641 Lecture, Dr. Lawlor
One common problem is to total up the values in an array. Serially, the code is trivial:
total=0;
for (int i=0;i<length;i++) total+=arr[i];
In
parallel, the problem is a lot harder--"total" is a sequential
bottleneck, since everybody has to add to it simultaneously. In
OpenMP, with a small number of threads, "reduction(+:total)" creates
private copies, and adds them up with atomic operations, but this
doesn't scale well to the many thousands of threads on a GPU, because
it takes time in O(p) for p processors.
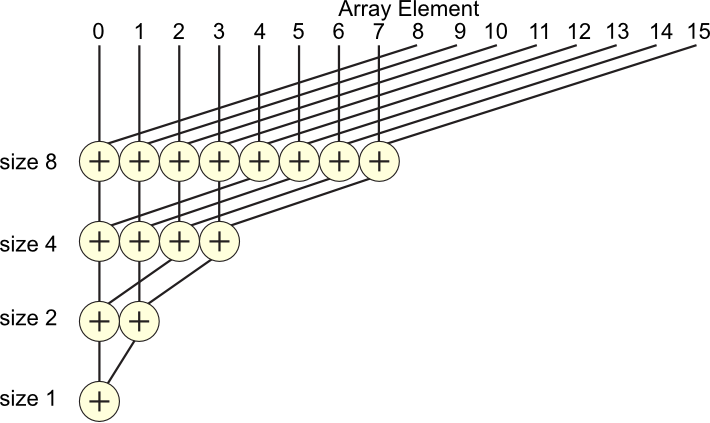
Another algorithm that scales much better is a tree-based summation,
shown here for 16 elements. To go from bottom up, we might begin
by summing pairs of two
elements, then summing across groups of four elements, then eight, and
finally all sixteen. This direction is useful for tree-based
networks, which have links along these paths, since most communication
is with your immediate neighbors.
![parallel prefix-like tree summation (reduction) [image is derivative work from public domain WikipediaFile:Prefix_sum_16.svg]](tree_sum_16.png)
To go from top down, you might first reduce the 16 element array to an
8 element array, then reduce that to a 4 element array, and so
on. But it's not a clear performance winner:
- For top down, the set of active elements is scattered across the
machine. This is good for heat dissipation, but it may hurt
branch locality depending on how elements get activated.
- For bottom up, the set of active elements is contiguous.
This is a little simpler to write in many GPU languages, and makes the
parallel cache coherence problem a bit easier to solve. Yet access locality is reduced,
because most reads are to distant elements (crossing the machine).
The code for the bottom-up version is:
GPU_KERNEL(
totalFloats,(__global<float *> arr,int length,int step),
{
int srcIdx=step*i+step/2;
if (srcIdx<length)
arr[step*i]+=arr[srcIdx];
}
)
/* Total up the n values in this array into arr[0].
Does this recursively, using log(n) kernel invocations. */
void totalArray(gpu_vector<float> &arr,int n)
{
for (int step=2;step/2<n;step*=2) {
totalFloats(arr,n,step).run((n+step-1)/step);
}
}
And a top-down version. This could be implemented by calling a
log number of kernels, like above. But it's quite a bit faster to
do a single kernel call with a loop on the GPU, for either bottom-up or
top-down:
/* Top-down version, with loop on the GPU */
GPU_KERNEL(
topdownAllFloats,(__global<float *> arr,int n),
{
while (n>1) {
int stride=(n+1)/2; // round up to find memory offset
int srcIdx=i+stride;
if (srcIdx<n)
arr[i]+=arr[srcIdx];
barrier(CLK_GLOBAL_MEM_FENCE); /* subtle: needed so we can read newly added values */
n=stride; /* new size is everything except what we've already read */
}
}
)
(Try this in NetRun now!)
On the NetRun GTX 280, this gives:
OpenCL initialized with 30 compute units
seq CPU total=8.00104e+06 (421.938us)
seq GPU total=8.00104e+06 (2853.99us)
bottom-up total=8.00184e+06 (345.965us)
topdown monokernel total=8.00184e+06 (170.045us)
Analytic total=8.00184e+06
Note
that
even with a small 8000-entry array, a sequential linear
summation is disaster on the GPU. It's pretty fast on the CPU
because the CPU is optimized for single-processor performance.
Either recursive version is much faster, O(lg n) versus O(n), and more
accurate
(due to roundoff). Both
effects just get worse as the array gets bigger.
You can do even better yet by putting the lower levels of the tree
summation into GPU "__local__" memory, which allows you to use local
thread synchronization instead of calling a second kernel, and by
running the highest levels of the tree on the CPU, where sequential
summation is faster. But both of these implementation adjustments
just tweak the asymptotic constant--the big speedup is using a good
parallel algorithm!
![parallel prefix-like tree summation (reduction) [image is derivative work from public domain WikipediaFile:Prefix_sum_16.svg]](tree_sum_16.png)
