Refracted Rays, Snell's Law, and Fresnel

CS 481 Lecture, Dr. Lawlor

So curiously enough, light's speed changes depending on what the light is moving through. This speed change changes the wavelength of the light. For example, red light has a wavelength of 650nm in air, but the same light has a wavelength of only 260nm in diamond, because light travels about 2.5 times more slowly through diamond than through air.

This wavelength change has a very strange effect when light passes out of one material and into another material. The wavelength changes, but wave crests can't be created or destroyed at the interface, so to make the waves match up, the light has to change direction. Here's a picture of what's going on:
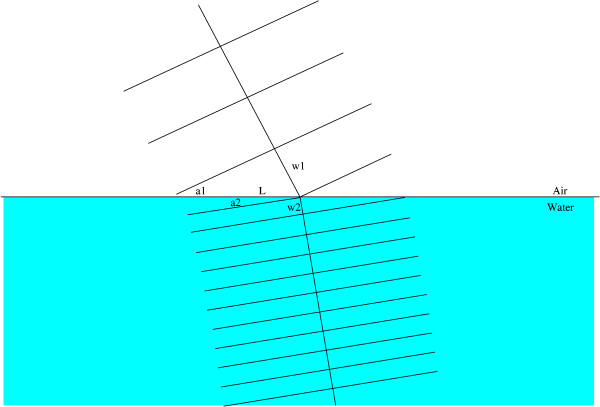
Derivation of Snell's Law

Here w1 is the wavelength in material 1, w2 is the wavelength in material 2, L is half the width of incoming light on the surface, and a1 and a2 are the angles between the wave fronts and the surface. a1 and a2 are also the angles between the light direction and surface normal!

It's just a bit of trig to figure out that
    sin(a1) = w1 / L
and
    sin(a2) = w2 / L

And dividing the two equalities above, we get
    sin(a1)/sin(a2) = w1/w2

This is called "Snell's Law"--the ratio of sines is the ratio of wavelengths, which is also the ratio of light speeds in the two materials. In fact, the speed of light in air divided by the speed of light in a material is called the material's "Index of Refraction". A higher refractive index means slower light, smaller wavelengths, and hence more light bending. Water's index of refraction is a mild 1.3; diamond's is a high 2.4 (this is what makes diamonds sparklier than ice).

In a raytracer, it's easy enough to compute refraction. In GLSL, there's even a builtin routine "refract" that takes the incoming (camera to object) direction, surface normal, and "eta" (relative index of refraction), and computes the refracted vector.
    float eta=1.0/1.4; // air/glass's index of refraction
    vec3 refractDir = refract(rayDir, hit_normal, eta);

It's easy enough to drop this direction computation into a raytracer! About the only tricky part is keeping track of the current index of refraction--when you're leaving a surface (normal and ray direction point in same direction), then you need to flip around not only the normal, but the indicies of refraction too. A production-quality raytracer will keep track of the index of refraction from the last-hit object, and shoot multiple rays for a dispersive material with different index of refraction for each wavelength--this causes the different wavelengths (colors) to separate out, like in a rainbow or prism.

One complication is that while exiting a more dense material, for near-grazing angles Snell's law has no solutions because sin(a2) would have to be greater than 1. In this case, instead of refracting out of the material, the light reflects back into the material, called "Total Internal Reflection". This is visible underwater, where the outside world is compressed into a small cylinder overhead, beyond which you only see underwater objects reflected upwards (for example, this reflected turtle). Total internal reflection is used in fiber optic cables, since it's a 100% efficient process. In a raytracer, the GLSL "refract" returns a zero-length vector in the case of total internal reflection. You need to manually check for this case, and fall back to reflection then.

$Water droplet showing refraction and total internal reflection.$
These water droplets show refraction on top, where the light rays bend down and hit the paper. After a wavelength-dependent transition region, the bottom of each droplet shows total internal reflection, where the light rays bounce off the bottom and back up into the room.

When underwater looking up, refraction compresses the whole aboveground world into a fairly small disk directly overhead. Outside the disk, total internal reflection shows only the sides of the pool.

Recently, "metamaterials" using structured grids of little conductive reflectors have achieved negative index of refraction, where a wave entering from the left side refracts to the left side, instead of bending to the right at a different angle.

Fresnel Reflectance and Refractance

In addition to the direction change when entering a new material (computed by Snell's law), there's a brightness tradeoff between reflected and refracted light. The Fresnel formulas can be used to compute the actual relative brightness of the reflected and refracted light, but they're pretty ugly to use:

The fresnel formulas, though physically accurate, are really slow.
Light's actual behavior depends on polarization, which we usually don't want to mess with. (Though there are polarized raytracers.)

However, the overall behavior of the fresnel equations is pretty important--the bottom line is that the steeper the incoming light (closer to parallel to the surface, perpendicular to the normal, the more reflection you get and the less refraction).

So there's a sort of cottage industry of "graphics-quality" approximations to the fresnel formulas. One classic approximation looks a heck of a lot like Phong shading--
float reflectivity=pow(1.0-clamp(dot(N,I),0.0,1.0),4.0);
That is, the reflectivity is near zero if we're looking straight down on the surface (N and I parallel, dot product near 1); and near 1.0 if we're looking at right angles to the surface (N and I near perpendicular, dot product near 0).

This sort of thing is also easy to drop into a raytracer.