Histograms, Coincidence, and Correlation

/*
 Binary file byte-coincidence histogramming tool.

 Dr. Orion Sky Lawlor, lawlor@alaska.edu, 2013-01-28 (Public Domain)
*/
#include <iostream>
#include <fstream>
#include <string>
#include <cmath>

double clamp(double v) {
	if (v<0.0) return 0.0;
	if (v>1.0) return 1.0;
	else return v;
}

class histo2d {
public:
	enum {n=256}; // byte histogram
	unsigned int data[n][n]; /* [first byte][next byte] */
	int last;
	
	histo2d() { // zero the histogram
		for (int i=0;i<n;i++)
		for (int j=0;j<n;j++)
			data[i][j]=0;
		last=-1;
	}
	
	void add(unsigned char next) {
		if (last!=-1) data[last][next]++;
		last=next;
	}
	
	void save(std::string filename) 
	{ // save to a PPM file
		filename+=".ppm";
		std::ofstream of(filename.c_str(),std::ios_base::binary);
		of<<"P6\n"<<n<<" "<<n<<"\n255\n";
	
	// Find the biggest value (to scale output to bytes)
		unsigned int big=0;
		for (int i=0;i<n;i++)
		for (int j=0;j<n;j++)
			if (data[i][j]>big) big=data[i][j];
		double scale=1.0/big;
	
	// Scale the output to bytes, and write them to disk.
		for (int i=0;i<n;i++)
		for (int j=0;j<n;j++)
		{
			unsigned char out=255*clamp(-0.1*log(data[i][j]*scale));
			
			unsigned char out2=out;
			if (((i&0x1f)==0 || (j&0x1f)==0)) 
				out2*=0.75; // make grid lines
			of.write((char *)&out2,1);
			of.write((char *)&out2,1);
			of.write((char *)&out,1);
		}
	}	
};

int main(int argc,char *argv[]) {
	if (argc<=1) {
		std::cout<<"Usage: coincidence <input file...>\n";
		return 1;
	}
	
	for (int argi=1;argi<argc;argi++) {
		const char *fileName=argv[argi];
		std::cout<<"Histogramming file "<<fileName<<"\n";
		histo2d h;
		std::ifstream file(fileName,std::ios_base::binary);
		unsigned char c;
		while (file.read((char *)&c,1)) h.add(c);
		h.save(fileName);
	}
}

binary zeros: note the black dot in the upper left at (0,0).

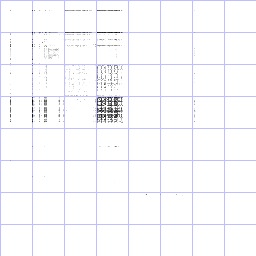
hexadecimal ASCII: numbers, lowercase letters, and newlines.

base64 text: lowercase, uppercase, punctuation, and newlines.

HP Lovecraft text: typical english text.  Note mostly lowercase, plenty of spaces.  Note the assymetry around capital letters--capital-lowercase occurs much more often than vice versa.

Wikipedia XML: more high ASCII/unicode, more punctuation, more complex structure.

tar-gzip file: Note classic binary fill-everywhere pattern.  White dot is intriguing.

zip file: similar to tar-gzip.  Biased toward lower numbers.

bz2 file: much less biased (better compression), although patterns still visible.

JPEG image: weird fine horizontal structures

MP3 Audio: relatively few heavily used codes.

/dev/urandom: almost perfectly uniform, except for random correlations.

AES-128 in CBC mode: looks perfectly uniform to me, even though we were encrypting just binary zeros.

AES-128 in ECB mode: uh-oh! That ain't random!