/*
SHA-256 Hash in C++
2013-02-19 : Orion Lawlor : Public domain
2010-06-11 : Igor Pavlov : Public domain
http://cpansearch.perl.org/src/BJOERN/Compress-Deflate7-1.0/7zip/C/Sha256.c
This code is based on public domain code from Wei Dai's Crypto++ library.
*/
#include <string.h> /* for size_t and memset (to zero) */
#include <string> /* for std::string */
/*
This class computes SHA256 message digests.
*/
class SHA256 {
public:
/* This type needs to be at least 32 bits, unsigned */
typedef unsigned int UInt32;
/* This is the type of the data you're processing */
typedef unsigned char Byte;
/* This is the data type of a message digest. */
class digest {
public:
enum {size=32}; // bytes in a message digest
SHA256::Byte data[size]; // binary digest data
// Equality. This is useful for "if (cur==target)" tests.
bool operator==(const digest &other) const {
for (int i=0;i<size;i++)
if (data[i]!=other.data[i])
return false;
return true;
}
// Less-than. This is mostly useful for std::map<SHA256::digest, ...>
bool operator<(const digest &other) const {
for (int i=0;i<size;i++)
if (data[i]<other.data[i])
return true;
else if (data[i]>other.data[i])
return false;
return false;
}
// Convert digest to an ASCII string of hex digits (for printouts)
std::string toHex() const;
};
/* External Interface */
SHA256(); // constructor. Sets up initial state.
// Add raw binary message data to our hash.
// You can call this repeatedly to add as much data as you want.
void add(const void *data, size_t size);
// Finish this message and extract the digest.
// Resets so you can add the next message, if desired.
SHA256::digest finish(void);
~SHA256(); // destructor. Clears out state and buffered data.
/* Internal Interface (public, for debug's sake) */
// This is the internal state of the hash.
UInt32 state[8];
// This is how many message bytes we've seen so far.
size_t count;
// This buffers up to a whole block of data
Byte buffer[64];
// Reset to initial values.
void init();
// Process the finished block of data in "buffer"
void block();
};
/* This is the *really* easy version: given a string as input, return the digest as output.
std::cout<<"SHA-256: "<<SHA256_digest(someString).toHex()<<"\n";
*/
inline SHA256::digest SHA256_digest(const std::string &src) {
SHA256 hash;
hash.add(&src[0],src.length());
return hash.finish();
}
/************** Bit twiddling and round operations for SHA256 *************/
/* Define bit rotate operations. These work like:
UInt32 ror(UInt32 value,UInt32 bitcount)
*/
#ifdef _MSC_VER /* Windows bit rotate from standard library */
# include <stdlib.h>
# define rol(x, n) _rotl((x), (n))
# define ror(x, n) _rotr((x), (n))
#else /* portable (Linux, Mac, etc) bit rotate */
# define rol(x, n) (((x) << (n)) | ((x) >> (32 - (n))))
# define ror(x, n) (((x) >> (n)) | ((x) << (32 - (n))))
#endif
/* These are the round keys, one per round. */
static const SHA256::UInt32 K[64] = {
0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5,
0x3956c25b, 0x59f111f1, 0x923f82a4, 0xab1c5ed5,
0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3,
0x72be5d74, 0x80deb1fe, 0x9bdc06a7, 0xc19bf174,
0xe49b69c1, 0xefbe4786, 0x0fc19dc6, 0x240ca1cc,
0x2de92c6f, 0x4a7484aa, 0x5cb0a9dc, 0x76f988da,
0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7,
0xc6e00bf3, 0xd5a79147, 0x06ca6351, 0x14292967,
0x27b70a85, 0x2e1b2138, 0x4d2c6dfc, 0x53380d13,
0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85,
0xa2bfe8a1, 0xa81a664b, 0xc24b8b70, 0xc76c51a3,
0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070,
0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5,
0x391c0cb3, 0x4ed8aa4a, 0x5b9cca4f, 0x682e6ff3,
0x748f82ee, 0x78a5636f, 0x84c87814, 0x8cc70208,
0x90befffa, 0xa4506ceb, 0xbef9a3f7, 0xc67178f2
};
/* This sets up the Sha256 initial state, at the start of a message. */
void SHA256::init()
{
state[0] = 0x6a09e667;
state[1] = 0xbb67ae85;
state[2] = 0x3c6ef372;
state[3] = 0xa54ff53a;
state[4] = 0x510e527f;
state[5] = 0x9b05688c;
state[6] = 0x1f83d9ab;
state[7] = 0x5be0cd19;
count = 0;
}
SHA256::SHA256() {
init();
}
unsigned int ROUND_COUNT=64; // HACK
/* This adds another block of data to our current state.
This is our main transforming/mixing function. */
void SHA256::block()
{
unsigned i;
UInt32 KWi[64]; // Per-round key + work data
// First part of W is just the incoming message data */
#define s0(x) (ror(x, 7) ^ ror(x,18) ^ (x >> 3))
#define s1(x) (ror(x,17) ^ ror(x,19) ^ (x >> 10))
UInt32 W[16]; // Work buffer: 0-15 are straight from the data
for (i = 0; i < 16; i++) {
W[i]=
((UInt32)(buffer[i * 4 ]) << 24) +
((UInt32)(buffer[i * 4 + 1]) << 16) +
((UInt32)(buffer[i * 4 + 2]) << 8) +
((UInt32)(buffer[i * 4 + 3])); // big-endian 32-bit load
KWi[i]=W[i]+K[i];
}
// The rest of W is a scrambled copy of the original data
for (;i<ROUND_COUNT;i++)
{
W[i&15] += s1(W[(i-2)&15]) + W[(i-7)&15] + s0(W[(i-15)&15]);
KWi[i] = W[i&15]+K[i];
}
UInt32 a,b,c,d,e,f,g,h; /* local copies of state, for performance */
a=state[0]; b=state[1]; c=state[2]; d=state[3];
e=state[4]; f=state[5]; g=state[6]; h=state[7];
// This is the main data transform loop
for (i = 0; i < ROUND_COUNT; i++) {
// SHA-256 round function:
// Mixing
h += (ror(e,6)^ror(e,11)^ror(e,25)) + (g^(e&(f^g))) + KWi[i]; // "Ch"
d += h;
h += (ror(a,2)^ror(a,13)^ror(a,22)) + ((a&b)|(c&(a|b))); // "Maj"
// Cyclic shift of variables:
UInt32 old_h=h;
h=g; g=f; f=e; e=d; d=c; c=b; b=a; a=old_h;
}
// Add result back into state array
state[0]+=a; state[1]+=b; state[2]+=c; state[3]+=d;
state[4]+=e; state[5]+=f; state[6]+=g; state[7]+=h;
/* Wipe temporary variables, for paranoia */
memset(W, 0, sizeof(W));
memset(KWi, 0, sizeof(KWi));
}
// Add raw binary message data to our hash.
void SHA256::add(const void *data, size_t size)
{
const Byte *dataptr=(const Byte *)data;
UInt32 curBufferPos = (UInt32)count & 0x3F; /* location within last block */
while (size > 0)
{
buffer[curBufferPos++] = *dataptr++; // copy next byte of data
count++; // message got longer
size--; // user data got shorter
if (curBufferPos == 64) // we have one whole block finished
{
curBufferPos = 0;
block();
}
}
}
/* End Sha256 processing, and write out message digest. */
SHA256::digest SHA256::finish(void)
{
size_t lenInBits = (count << 3); // i.e., times 8 bits per byte
UInt32 curBufferPos = (UInt32)count & 0x3F; // 0x3f is mask to wrap around to buffer size
unsigned i;
buffer[curBufferPos++] = 0x80; // standard specifies "add a one bit...
while (curBufferPos != (64 - 8)) // ...then pad with zeros to end of block"
{
curBufferPos &= 0x3F;
if (curBufferPos == 0)
block();
buffer[curBufferPos++] = 0; // zero out rest of block
}
// Finally, add message length, in bits, as big-endian 64 bit number
for (i = 0; i < 8; i++)
{
buffer[curBufferPos++] = (Byte)(lenInBits >> 56);
lenInBits <<= 8;
}
block(); // transform last block (including length)
// Copy state out as big-endian integers.
SHA256::digest output;
for (i = 0; i < 8; i++)
{
output.data[i*4+0] = (Byte)(state[i] >> 24);
output.data[i*4+1] = (Byte)(state[i] >> 16);
output.data[i*4+2] = (Byte)(state[i] >> 8);
output.data[i*4+3] = (Byte)(state[i]);
}
init(); // reset for next trip around
return output;
}
SHA256::~SHA256()
{
// To keep from leaving any sensitive data lying around, zero out our buffers.
memset(state,0,sizeof(state));
count=0;
memset(buffer,0,sizeof(buffer));
}
std::string SHA256::digest::toHex() const
{
std::string ret="";
for (int i=0;i<size;i++) {
const char *hexdigit="0123456789abcdef";
ret+=hexdigit[(data[i]>>4)&0xf]; // high 4 bits
ret+=hexdigit[(data[i] )&0xf]; // low 4 bits
}
return ret;
}
/***** Actual user code ****/
std::string str="!";
int digest_short() { return SHA256_digest(str).data[0]; }
int foo(void) {
print_time("hash time",digest_short);
std::cout<<SHA256_digest("0").toHex()<<"\n";
return 0;
}
Here's a very weakened version of SHA-256 using *zero* rounds,
showing the hash of each the digits 0-9. Because we don't
touch the original data (that happens in the rounds), the output
is constant. Collision city!
d413ccce76cf5d0a78dde6e44a9fea74a21ca4fe360ad1183f07b356b7c19a32 d413ccce76cf5d0a78dde6e44a9fea74a21ca4fe360ad1183f07b356b7c19a32 d413ccce76cf5d0a78dde6e44a9fea74a21ca4fe360ad1183f07b356b7c19a32 d413ccce76cf5d0a78dde6e44a9fea74a21ca4fe360ad1183f07b356b7c19a32 d413ccce76cf5d0a78dde6e44a9fea74a21ca4fe360ad1183f07b356b7c19a32 d413ccce76cf5d0a78dde6e44a9fea74a21ca4fe360ad1183f07b356b7c19a32 d413ccce76cf5d0a78dde6e44a9fea74a21ca4fe360ad1183f07b356b7c19a32 d413ccce76cf5d0a78dde6e44a9fea74a21ca4fe360ad1183f07b356b7c19a32 d413ccce76cf5d0a78dde6e44a9fea74a21ca4fe360ad1183f07b356b7c19a32 d413ccce76cf5d0a78dde6e44a9fea74a21ca4fe360ad1183f07b356b7c19a32
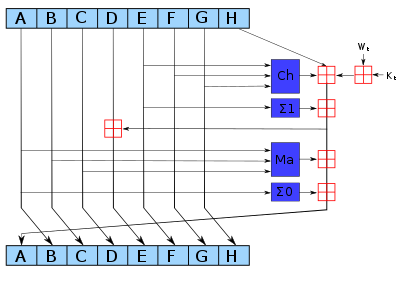
Using one round, there are only two localized places with differences, where the data was added in.
d413ccce76cf5d0a78dde6e46e97d7dca21ca4fe360ad1183f07b35688695566 d413ccce76cf5d0a78dde6e46f97d7dca21ca4fe360ad1183f07b35689695566 d413ccce76cf5d0a78dde6e47097d7dca21ca4fe360ad1183f07b3568a695566 d413ccce76cf5d0a78dde6e47197d7dca21ca4fe360ad1183f07b3568b695566 d413ccce76cf5d0a78dde6e47297d7dca21ca4fe360ad1183f07b3568c695566 d413ccce76cf5d0a78dde6e47397d7dca21ca4fe360ad1183f07b3568d695566 d413ccce76cf5d0a78dde6e47497d7dca21ca4fe360ad1183f07b3568e695566 d413ccce76cf5d0a78dde6e47597d7dca21ca4fe360ad1183f07b3568f695566 d413ccce76cf5d0a78dde6e47697d7dca21ca4fe360ad1183f07b35690695566 d413ccce76cf5d0a78dde6e47797d7dca21ca4fe360ad1183f07b35691695566By the second round, these differences are spread to parts of the next integer:
d413ccce76cf5d0ad92cb5606e97d7dca21ca4fe360ad118d546c95188695566 d413ccce76cf5d0a572055616f97d7dca21ca4fe360ad11853fa714e89695566 d413ccce76cf5d0ad72475617097d7dca21ca4fe360ad118d3be795a8a695566 d413ccce76cf5d0a5939155e7197d7dca21ca4fe360ad118569321538b695566 d413ccce76cf5d0ad93d355e7297d7dca21ca4fe360ad118e65768ff8c695566 d413ccce76cf5d0a5730d55f7397d7dca21ca4fe360ad118650b10fc8d695566 d413ccce76cf5d0ad734f55f7497d7dca21ca4fe360ad118e4cf19088e695566 d413ccce76cf5d0a6189956c7597d7dca21ca4fe360ad1186fe3c1118f695566 d413ccce76cf5d0ae18db56c7697d7dca21ca4fe360ad118efa808fd90695566 d413ccce76cf5d0a5f81556d7797d7dca21ca4fe360ad1186e5bb0fa91695566By the third round, another integer is changed:
d413ccce69df2c09d92cb5606e97d7dca21ca4fe9699b51bd546c95188695566 d413ccceebde983d572055616f97d7dca21ca4fee677b4b353fa714e89695566 d413ccce6bff0b91d72475617097d7dca21ca4feb84b5e71d3be795a8a695566 d413cccefdbc7be55939155e7197d7dca21ca4fe5e991720569321538b695566 d413ccce7d9c6a99d93d355e7297d7dca21ca4fe098b8ab2e65768ff8c695566 d413cccefc1e5d4d5730d55f7397d7dca21ca4fe7914b40f650b10fc8d695566 d413ccce7bbcca21d734f55f7497d7dca21ca4fea93e168be4cf19088e695566 d413ccce721ce8cd6189956c7597d7dca21ca4fed915bd1d6fe3c1118f695566 d413cccef33cb999e18db56c7697d7dca21ca4fee59e3517efa808fd90695566 d413ccce747d0a655f81556d7797d7dca21ca4fe3dcf9a8c6e5bb0fa91695566By the fourth round, it's more changes than not:
75a08fe669df2c09d92cb5606e97d7dc7bc4d2959699b51bd546c95188695566 d5bc67ffebde983d572055616f97d7dcfaffcf8de677b4b353fa714e89695566 c3a868676bff0b91d72475617097d7dc7c598f28b84b5e71d3be795a8a695566 a282c861fdbc7be55939155e7197d7dc520180d45e991720569321538b695566 67eddb9e7d9c6a99d93d355e7297d7dcdd855095098b8ab2e65768ff8c695566 40f7842afc1e5d4d5730d55f7397d7dcaa3442fe7914b40f650b10fc8d695566 c8336d4d7bbcca21d734f55f7497d7dc99f846dda93e168be4cf19088e695566 a47c01f1721ce8cd6189956c7597d7dcfdeeed45d915bd1d6fe3c1118f695566 cccb013af33cb999e18db56c7697d7dc701c5e04e59e3517efa808fd90695566 e689646c747d0a655f81556d7797d7dc1ace14c43dcf9a8c6e5bb0fa91695566By the fifth round, only a few places haven't been touched yet. These are hit by the sixth round.
75a08fe669df2c09d92cb5606a7d15517bc4d2959699b51bd546c95141e2fbdc d5bc67ffebde983d572055611675742ffaffcf8de677b4b353fa714e491f4cc5 c3a868676bff0b91d72475618b86d5a57c598f28b84b5e71d3be795aafeb4646 a282c861fdbc7be55939155e9d5833c5520180d45e9917205693215381b0cd4e 67eddb9e7d9c6a99d93d355e4c362b80dd855095098b8ab2e65768ffdc275793 40f7842afc1e5d4d5730d55fd6fcccf9aa3442fe7914b40f650b10fc9f9c717e c8336d4d7bbcca21d734f55fa3a8aea299f846dda93e168be4cf1908a93f0df4 a47c01f1721ce8cd6189956c8281c9abfdeeed45d915bd1d6fe3c11130e3f80b cccb013af33cb999e18db56c4d0a19d8701c5e04e59e3517efa808fdba51fb94 e689646c747d0a655f81556d410de3681ace14c43dcf9a8c6e5bb0fac2fec706(Try this in NetRun now!)
5feceb66ffc86f38d952786c6d696c79c2dbc239dd4e91b46729d73a27fb57e9 6b86b273ff34fce19d6b804eff5a3f5747ada4eaa22f1d49c01e52ddb7875b4b d4735e3a265e16eee03f59718b9b5d03019c07d8b6c51f90da3a666eec13ab35 4e07408562bedb8b60ce05c1decfe3ad16b72230967de01f640b7e4729b49fce 4b227777d4dd1fc61c6f884f48641d02b4d121d3fd328cb08b5531fcacdabf8a ef2d127de37b942baad06145e54b0c619a1f22327b2ebbcfbec78f5564afe39d e7f6c011776e8db7cd330b54174fd76f7d0216b612387a5ffcfb81e6f0919683 7902699be42c8a8e46fbbb4501726517e86b22c56a189f7625a6da49081b2451 2c624232cdd221771294dfbb310aca000a0df6ac8b66b696d90ef06fdefb64a3 19581e27de7ced00ff1ce50b2047e7a567c76b1cbaebabe5ef03f7c3017bb5b7This is the "avalanche effect".