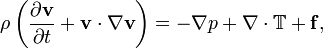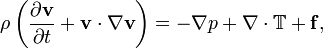Vector Partial Differential Equations & Navier-Stokes

CS 493 Lecture, Dr. Lawlor

Vector Calculus: Div, Grad, Curl

For reference, you often see these vector calculus symbols in PDEs:

Symbol	Pronounced	Mathematical Definition	Input Output	Meaning
∇A	"gradient A" "grad A" or "del A"	vec3(∂A / ∂x, ∂A / ∂y, ∂A / ∂z)	scalar vector	The gradient vector points in the direction of greatest change.
∇ . A	"divergence A" or "div A"	∂A.x / ∂x + ∂A.y / ∂y + ∂A.z / ∂z	vector scalar	Positive divergence indicates areas where a vector field is leaving. Negative indicates convergence, where field is arriving.
∇ . ∇ A or ∇²A or ∆A	"laplace A" or "div grad A"	∂²A / ∂x² + ∂²A / ∂y² + ∂²A / ∂z²	scalar scalar	The Laplace operator shows up in diffusion, and other energy minimization problems.
∇ x A	"curl A" "vorticity A" or "rot A"	vec3(∂A.z / ∂y - ∂A.y / ∂z, ∂A.x / ∂z - ∂A.z / ∂x, ∂A.y / ∂x - ∂A.x / ∂y)	vector vector	The curl operator measures local rotation. The magnitude of the curl indicates rotational speed. The direction of the curl indicates the rotational axis.

Navier-Stokes Fluid Dynamics

For example, Navier-Stokes fluid dynamics is:
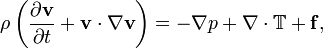
$navier stokes equation$

The variables here are easy enough:

v is the fluid velocity. It's a vector, and hence written in bold.
$ρ$ , the Greek letter rho, is the fluid density: mass/volume. It's there because this equation is actually "m * A = F" (rearranged F=mA).
p is the fluid pressure.
T is a stress tensor, used for viscous fluids. If viscosity is zero, you can ignore this term.
f are any other forces acting on the fluid, like gravity or wind. Calling these "body forces" makes them sound more mysterious and intimidating.

As we saw above, "∇ p" means a gradient:

∇ p = del p = vec3(∂p / dx, ∂p / dy, ∂p / ∂z)

This converts a scalar pressure, into a vector pointing in the direction of greatest change. The magnitude of the vector corresponds to the pressure difference.

We've seen this "pressure derivatives affect velocity" business in our little wave simulation program, where we're updating the current velocity:

vel.x+=dt*(L.z-R.z); /* height difference -> velocity */
vel.y+=dt*(B.z-T.z);

Written more mathematically, we're really doing this computation.

dv / dt = vec2(L.b-R.b,B.b-T.b)

Recall that from the Taylor series, we can approximate the pressure derivative with a centered difference dp/dx = (R.b-L.b)/grid_size. Say both the grid size and fluid density

ρ

both equal one. This means our simple wave simulation code is actually computing

ρ

dv / dt = vec2(L.b-R.b,B.b-T.b) = -vec2(∂p/∂x,∂p/∂y) = - del p = - ∇ p

Hey, that's exactly the leftmost terms on both sides in Navier-Stokes!

Bulk Transport: Advection

We now move on to "v · ∇ v", the term of the Navier-Stokes equations that represents moving fluid--this is called various things like convection (when driven by heat), advection (when driven by anything else), or just "wind" or "bulk transport".

Now, "∇ v" is the gradient of the velocity: vec3( ∂v/∂x, ∂v/∂y, ∂v/∂z). This is a little odd, because velocity is already a vector, so taking the gradient gives us a vector of vectors (a matrix, or tensor). Dotting this vector of vectors in "v · ∇ v" gives us a vector again, which is good because it's being added to dv/dt, which is also a vector. The bottom line is:

v · ∇ v = dot(v,vec3( ∂v/∂x, ∂v/∂y, ∂v/∂z)) = v.x * ∂v/∂x + v.y * ∂v/∂y + v.z * ∂v/∂z

In English, we're dotting our vector field with its own gradient. This tells us how similar the vectors are to the direction of greatest change, which in turn says how much the value of the vector will change when moving in that direction. That's how "v · ∇ v" simulates fluid transport.

Now, we could implement this by actually taking some finite difference approximation of ∂v/∂x and actually computing the vector v · ∇ v at each pixel, but this approach tends to break down and go unstable if the velocity gets too big. The problem with the differential approximation to transport is that it fits a linear model to the local velocity neighborhood; moving by more than one pixel is essentially using linear extrapolation, which will amplify small waves in the mesh. (The curious can read about the Courant-Fredrichs-Lewy (CFL) condition.)

On the graphics hardware, it's actually a lot easier to move stuff around onscreen by just changing your texture coordinates--normally, you look "upwind" against the flow to see where your values are coming from:

vec4 C = texture2D(srcTex,texCoords); /* center pixel, for vel estimate */
vec2 dir = C.xy; /* my velocity */
vec2 tc = texCoords - vel*dir; /* move "upwind" */
C = texture2D(srcTex,tc); /* advected source center pixel */

This also gives advection just like v · ∇ v, but it's more error-tolerant than v · ∇ v, because we can advect by multiple pixels in a single step. Jos Stam calls this technique "stable fluids".

Overall, the bottom line on Navier-Stokes is actually pretty simple:
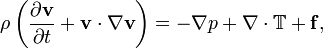
$navier stokes equation$
density * ( acceleration + advection) = pressure induced forces + viscosity induced forces + other forces