Lecture Note from UAF Computer Science
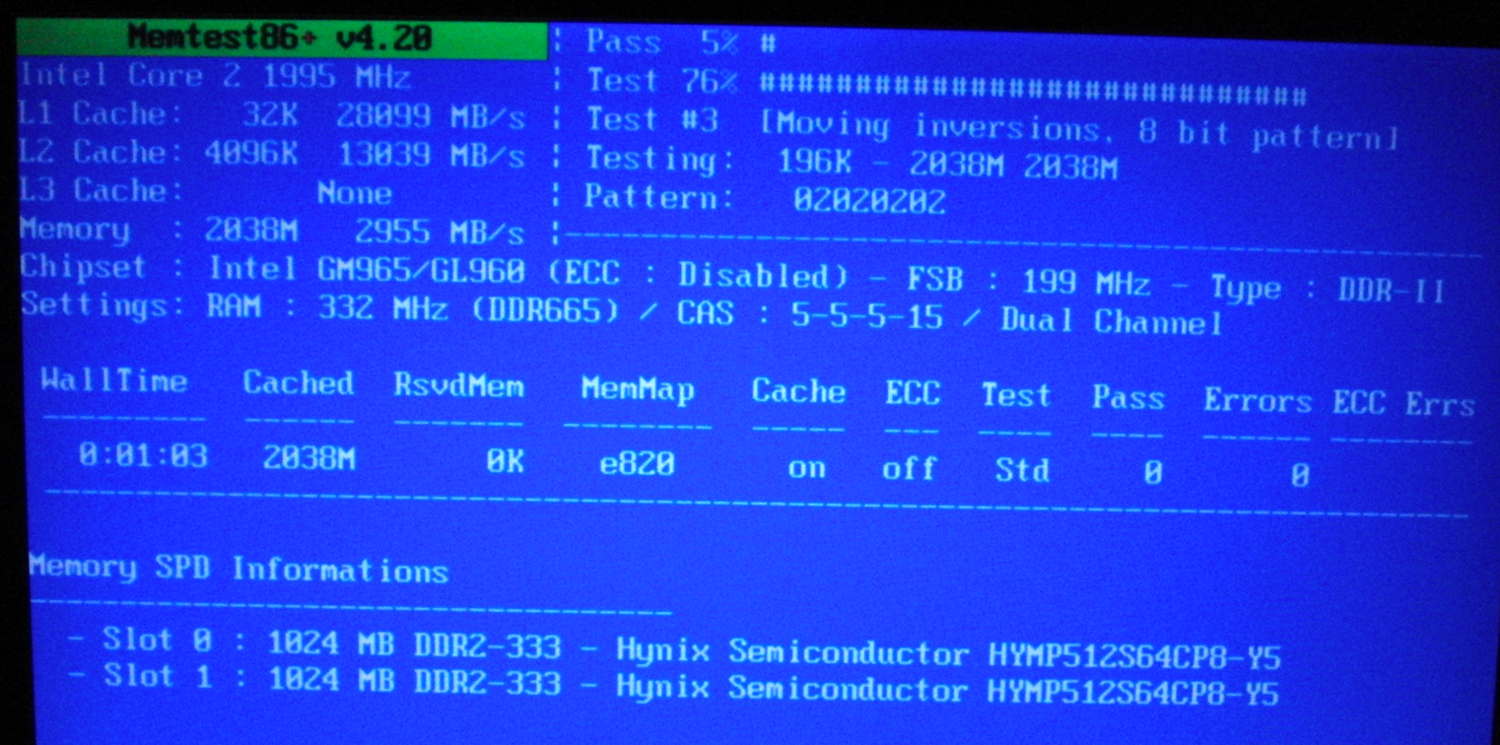
Here's a screenshot from Memtester on a 2GHz Core 2 laptop. Note how:
L1 cache is only 32KB, but can be read at 28GB/sec.
L2 cache is larger, 4MB, but can be read at 13GB/sec.
RAM is much bigger, 2GB, but only 3GB/sec.

The gate design of a cache is surprisingly subtle. This is a 4-line single-byte cache, and I've omitted the process by which cache lines are allocated, and data is written into the cache. Download the .circ file for Logisim here.
In a real CPU, the cache hit line is used to stall the pipeline if the data being read is not in the cache, and activate a fetch out to RAM.
In a real CPU, cache uses 32 byte or 64 byte cache lines (this saves tag bits), and stores thousands of lines. Because a fully associative comparator like above would get very expensive for thousands of lines, a real cache is "set associative", allowing a given address to live in only one of a few possible cache lines, such as a 4-way associative cache using the comparator circuit above.
Anytime you have a cache, of any kind, you need to figure out what to do when the cache gets full. Generally, you face this problem when you've got a new element X to load into the cache--which cache slot do you place X into?
The simplest approach is a "direct mapped cache", where element X goes into cache slot X%N (where N is the size of the cache). Direct mapping means elements 1 and 2 will go into different adjacent slots, but you can support many elements.
For example, the Pentium 4's L1 cache was 64KB in size and direct-mapped. This means address 0x0ABCD and address 0x1ABCD (which are 64KB apart) both get mapped to the same place in the cache. So even though this program was very fast (5.2ns/call):
enum {n=1024*1024};
char arr[n];
int foo(void) {
arr[0]++;
arr[12345]++;
return 0;
}
By contrast this very similar-looking program was very slow (20+ns/call), because both array elements (exactly 64KB apart) map to the same line of the cache, so the CPU keeps overwriting one with the other (called "cache thrashing"), and the cache is totally useless:
enum {n=1024*1024};
char arr[n];
int foo(void) {
arr[0]++;
arr[65536]++;
return 0;
}
In general, power-of-two jumps in memory can be very slow on direct-mapped machines. This is one of the only cases on computers where powers of two are not ideal!
More recent machines avoid the thrashing of a direct-mapped cache by allowing a given memory address to sit in one of two or four slots, called two- or four-way "set associative caching" (described here, or in the Hennessy & Patterson book, Chapter 7). On such machines, you can still get cache thrashing with power of two jumps, but you need more and longer jumps to do so.
For example, my Skylake i7-6700K has a 16-way set associative L3 cache , so this program is unexpectedly slow:
enum {n=100*1024*1024};
char arr[n];
int foo(void) {
int stride=65536; //<- power of two = same set in set-associative cache
for (int copy=0;copy<16;copy++)
arr[stride*copy]++;
return 0;
}
Changing the stride results in much higher performance, because all 16 copies aren't fighting for the same set in the set-associative cache.
In general, there are many more complicated cache replacement algorithms, although most of them are too complicated to implement in hardware. The OS treats RAM as a cache of data on disk, and since disks are so slow, it can pay to be smart about choosing which page to write to disk.
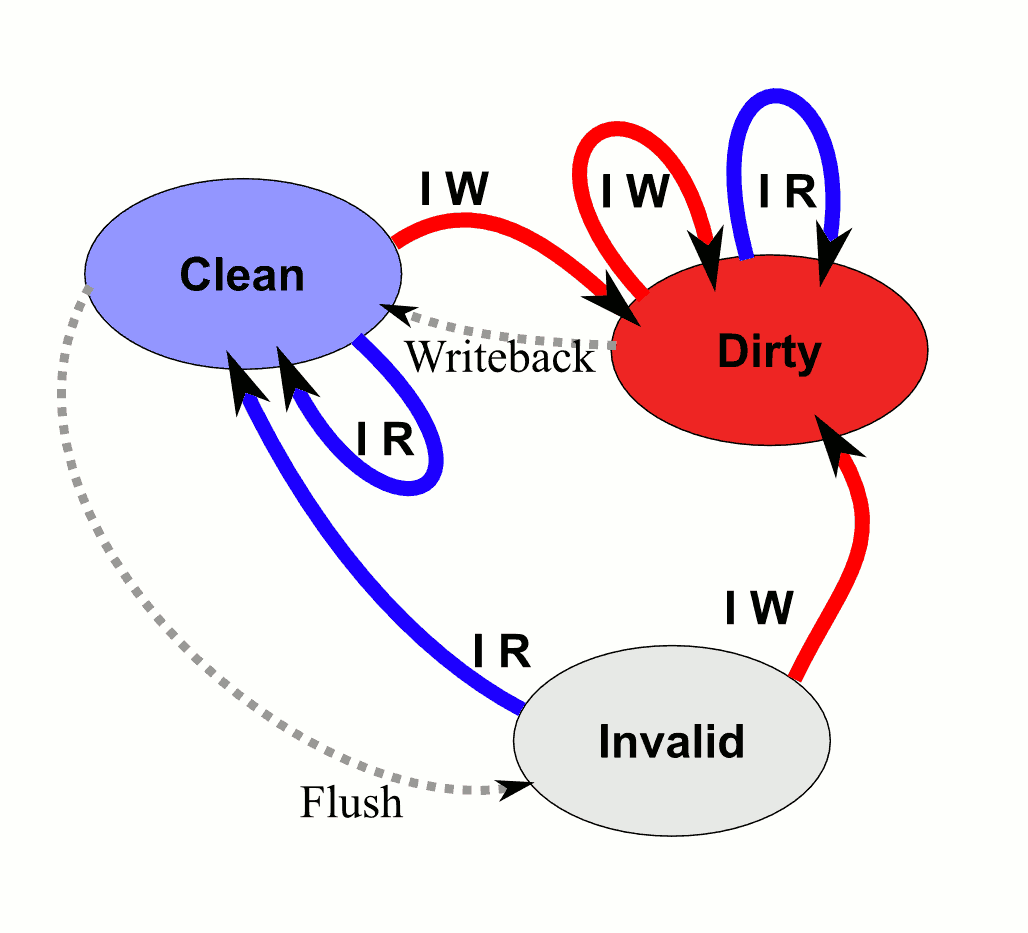
Given cache writes, here's a cache line's state diagram:
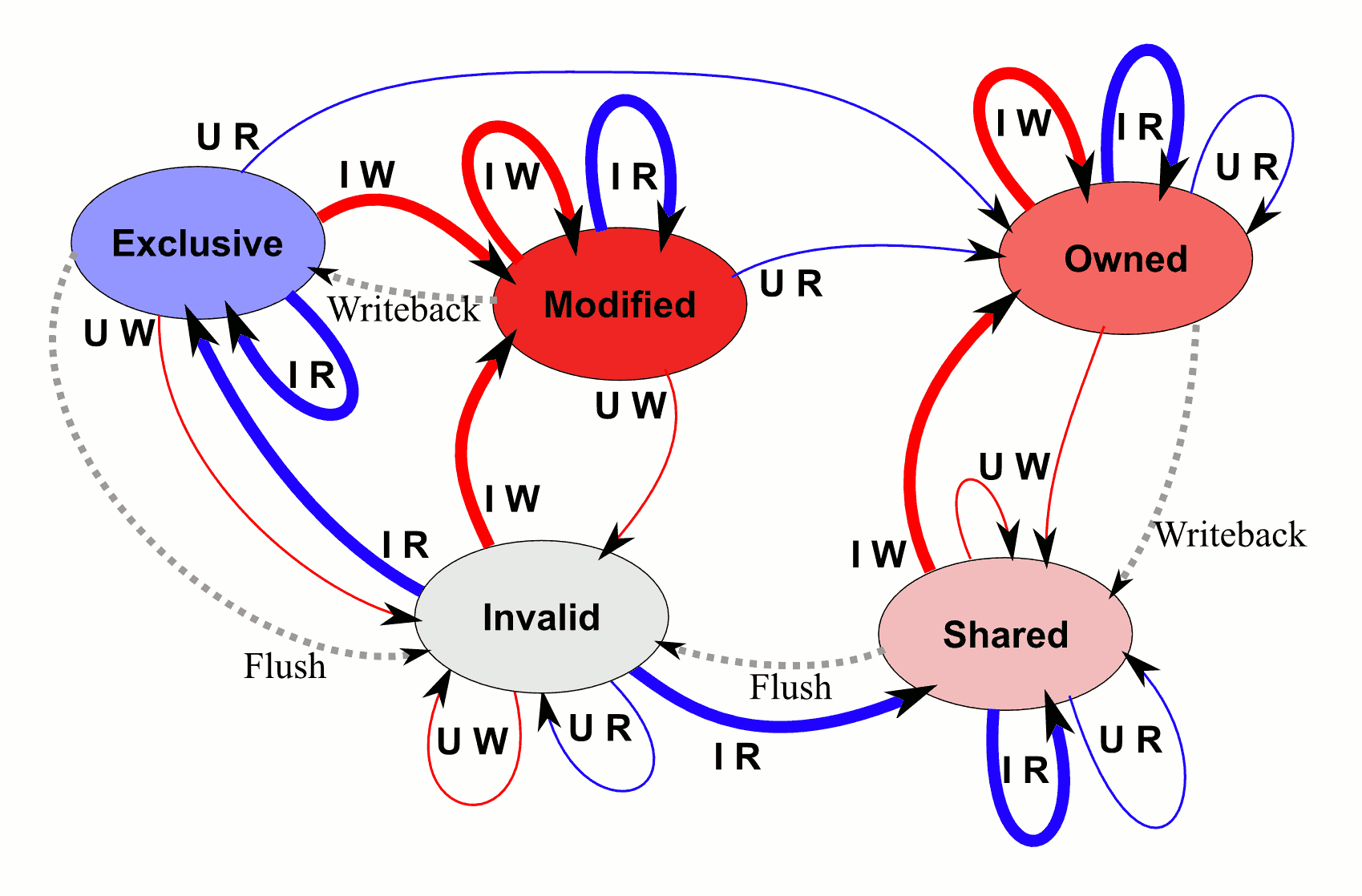
In a multicore machine, you need a cache coherence protocol CPUs use to ensure that writes to different locations will combine properly. This amounts to adding states to deal with reads and writes from other cores. This is a variant of MOESI:
Why do you care? If two threads access the *same* data, you need to worry about locking or atomic operations to get the right answer. But if two threads write to *adjacent* data, in the same 64-byte cache line, cache coherence traffic above gives you the right answer, but at the price of performance loss due to this "false sharing". If two threads access data in separate cache lines, more than 64 bytes apart, you get the right answer with good performance!
#include <thread>
enum {n=1000*1000}; // a large number, to outweigh thread creation overhead
volatile int arr[128]; // place in memory threads do their work
// Trivial approximation of useful work done by a thread
void do_work(int my) {
for (int i=0;i<n;i++) arr[my]++;
}
int foo(void) {
arr[0]=0;
std::thread t(do_work,16); // 16 ints == 64 bytes, one cache line away
do_work(0);
t.join();
return arr[0];
}
This code shows perfect scalability, with two threads doing twice the work in the same amount of time, only if the other threads are far enough apart in the work array. If you modify the 16 above to 1, you get about a 50% slowdown!
Larger machines, where there is no shared bus, usually have non-uniform memory access: local memory is faster to access than remote memory. To keep track of the caches, NUMA machines usually use some form of directory protocol, where there's a tiny stub associated with each potential cache line in memory, telling you the CPU responsible for keeping track of that cache line, or -1 if it's uncached.
You can even write your own distributed shared memory cache coherence protocol, using local RAM as a cache for remote RAM. Typically the "cache line" size is the same as the size of a hardware page, say 4KB for x86. This is pretty big, so to avoid false sharing on SDSM systems, you need to make sure different threads' data is many kilobytes separated!
CS 441 Lecture Note, 2014, Dr. Orion Lawlor, UAF Computer Science Department.