Here is the "best of" HW#1 solutions and a guide to what you need to
do for HW#4.
Some general comments
- Before doing anything, use your experience/knowledge to predict
what you think the answer should be. If the result is completely
different, there is a good chance something is wrong and you
should do some additional investigation. BUT, don't force the
conclusion to be your
prediction - it might be you that needs to be corrected.
- Output units in your program! I should never just see a number that
represents time without a unit. And make sure to put them on any graphs.
Another analyst should be able to draw the same conclusions
as you do by looking at the graphs.
- On Unix systems use times(), which returns time in clocks ticks.
As to wall-clock vs user time, you need to pick the best one based
on your application/benchmark/etc. For example, use wall-clock if
the question is "how many sqrts can I do in one hour". Use user
time if the question is "what is the max number of sqrts I can do
in one hour and I'm willing/able to kick everyone off the system
and make sure this is the only program running".
- Nobody did a good job in determining clock resolution and the
effect on your results - hence HW#3. Everyone just used "a lot"
of loop iterations to the point that "it should be ok".
- The number of sqrt()s required was on the order of millions to
billions to reduce the clock resolution error.
- Timing the loop
for ( i=0 ; i<1000000 ; i++ ) a = sqrt( random_number(0.0,1.0) );
and subtracting the time for this loop:
for ( i=0 ; i<100000 ; i++ ) a = random_number(0.0,1.0);
wasn't accurate for most architectures.
If a CPU has a integer and floating point units (i.e. can be executing
both at the same time), the random number is being generated while
the CPU would be waiting for the previous sqrt to finish. This
results in a faster avg. sqrt time using the above loops.
Specific Example - 300MHz Mips R12000
4 runs averaged together - 58.78ns (wall clock) and 35.44ns (user time)
for calculating the square root with sqrt().
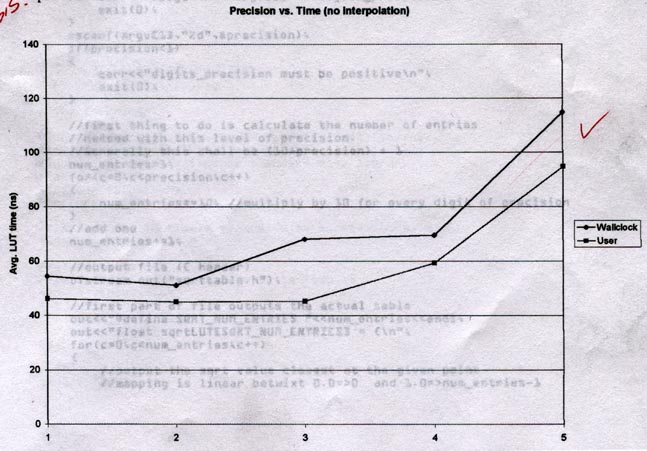
Notice the jump from 4 to 5 digits. Is 5 "just a little on the high
side" and would 6 be back following the slope of 1-4? This tells you
to try 6, 7, maybe even 8, until you know what happens. Multiple
runs at each precision would also give us a better idea of the "curve" -
is there really a 4x difference between wall-clock and user-time between
2 and 3 digits of precision?
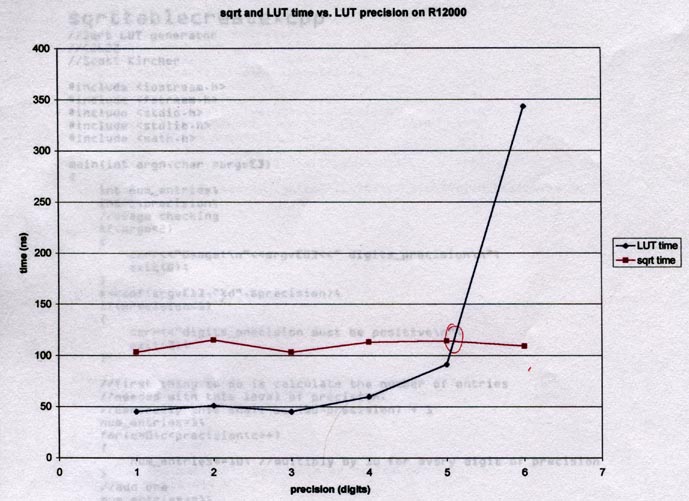
With a sample size of 1 at each point, it looks like LUT is 2x as fast
sqrt() for 1-4 digits of precision. We have a crossing near 5 and
a dramatic change (as we should have predicted) for 6 digits of precision.
To conclude this with more certainty, we need to take several samples
at each data point and calculate a confidence interval.
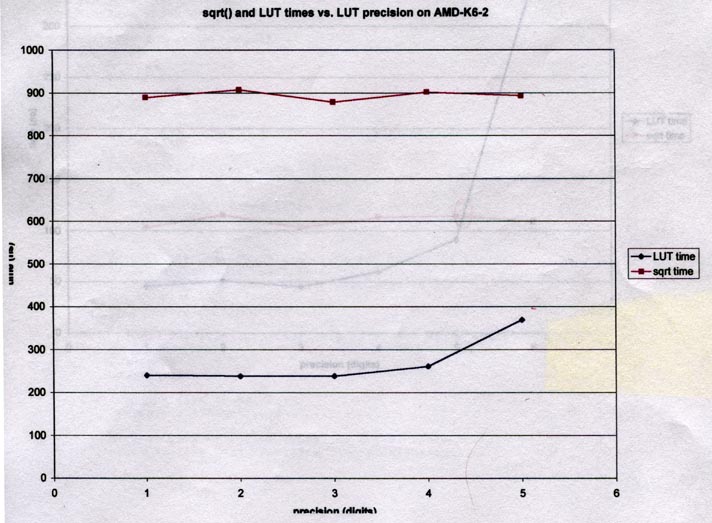
A different CPU (AMD) and I would say this doesn't have hardware support
for sqrt(). Because of this, LUT is 3-4 times faster than sqrt() for
1-4 digits of precision. I'd say 5 is still 2-3 times faster, but without
an idea of measurement error it could be random error. Again,
confidence bands (plot points c1 and c2 for each data point and draw
lines connecting the c1s and c2s) would give us a better idea.



